J.M.W. Turner: Sketchbooks, Drawings and Watercolours

ISBN 978-1-84976-386-8
J.M.W. Turner > 1802-18 Academician and professor > Perspective lectures c.1809-28 > III. Diagrams after Samuel Cunn's ... > Artwork

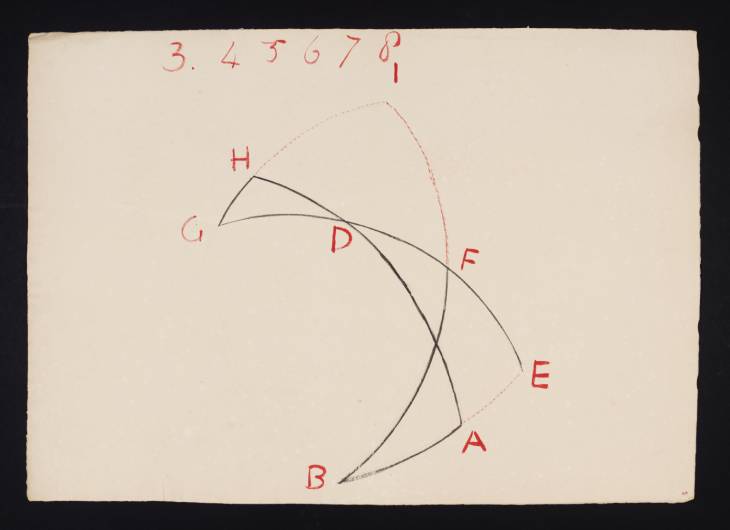
Joseph Mallord William Turner Lecture Diagram: 'Euclid's Elements of Geometry', Spherical Trigonometry, Propositions 25, 26, 27, 28, 29 and 30 c.1817-28

Joseph Mallord William Turner, ‘Lecture Diagram: 'Euclid's Elements of Geometry', Spherical Trigonometry, Propositions 25, 26, 27, 28, 29 and 30’ c.1817-28
Joseph Mallord William Turner 1775–1851
Lecture Diagram: ‘Euclid’s Elements of Geometry’, Spherical Trigonometry, Propositions 25, 26, 27, 28, 29 and 30 circa 1817–28
D17010
Turner Bequest CXCV 40
Pencil and watercolour on white wove paper, 488 x 693 mm
Watermarked ‘J WHATMAN | TURKEY MILLS | 1817’
Inscribed by Turner in red watercolour ‘3’, ‘4’, ‘5’, ‘6’, ‘7’, and ‘8’ along top and with various initial letters within diagram
Inscribed by John Ruskin in red ink ‘40’ bottom right
 
Accepted by the nation as part of the Turner Bequest 1856
Prepared in connection with his lectures as Professor of Perspective at the Royal Academy, Turner’s diagram is based on an illustration from Samuel Cunn’s Euclid’s Elements of Geometry (London 1759, Spherical Trigonometry). It illustrates Propositions 25, 26, 27, 28, 29, and 30 on Spherical Trigonometry. Cunn describes Proposition 25 as ‘In a spherical triangle A B C, right-angled at A, as the cosine of the angle B, at the base B A, is to the sine of the vertical angle A C B, so is the cosine of the perpendicular, to the radius’;1 Proposition 26 as ‘The cosine of the base : cosine of the hypothenuse : R :: cosine of the perpendicular’;2 Proposition 27 as ‘S, of the base : R :: T, of the perpendicular : T, of the angle at the base’; Proposition 28 as ‘cosine of the vertical angle : R : : T, of the perpendicular : T, of the hypothenus’;3 Proposition 29 as ‘S, of the hypothenus : R :: S, of the perpendicular : S, of the angle at the base’;4 and Proposition 30 as ‘R : cosine of the hypothenus : : T, of the vertical angle : cot. of the angle at the base’.5 There are sketches of the diagram in Turner’s lecture notes.6
1
Cunn 1759, p.303.
2
Ibid.
3
Ibid.
4
Ibid.
5
Ibid.
6
Turner, ‘Royal Academy Lectures’, circa 1807–38, Department of Western Manuscripts, British Library, London, ADD MS 46151 X folios 6 and verso, 7, 10 verso, 21.
Technical notes:
Peter Bower writes that the sheet is Super Royal size Whatman paper made by Finch and Thomas Robert Hollingworth, at Turkey Mill, Maidstone, Kent.1
1
Notes in Tate catalogue files.
Verso:
Blank, save for an inscription by an unknown hand in pencil ‘23’ bottom left.

Andrea Fredericksen
June 2004

Supported by The Samuel H. Kress Foundation

Revised by David Blayney Brown
January 2012

How to cite

Andrea Fredericksen, ‘Lecture Diagram: ‘Euclid’s Elements of Geometry’, Spherical Trigonometry, Propositions 25, 26, 27, 28, 29 and 30 c.1817–28 by Joseph Mallord William Turner’, catalogue entry, June 2004, revised by David Blayney Brown, January 2012, in David Blayney Brown (ed.), J.M.W. Turner: Sketchbooks, Drawings and Watercolours, Tate Research Publication, December 2012, https://www.tate.org.uk/art/research-publications/jmw-turner/joseph-mallord-william-turner-lecture-diagram-euclids-elements-of-geometry-spherical-r1136732, accessed 25 April 2024.